Table of Contents
Mathematics is an essential subject that every student must learn. Shapes are an essential part of mathematics, and it is essential to learn the names of shapes to understand the basics of geometry. Shapes are present in our daily lives, and knowing the names of shapes can be useful in many situations.
In this article, we will discuss 54 math names of shapes with pictures that will help students to learn about shapes in an easy and interactive way.
Circle:
A circle is a two-dimensional shape that is defined as a set of points that are equidistant from the center. It has no corners and is the same distance from the center at all points.

Square:
A square is a four-sided polygon with four equal sides and four right angles. It has four corners and is a type of rectangle.

Rectangle:
A polygon with four sides and four right angles is called a rectangle. It has two parallel sets of sides, and the lengths of the opposite sides are equal.

Triangle:
A polygon with three sides and three angles is a triangle. It has three corners and can be divided into many forms according to the width of its sides and the angles at which it is angled.

Rhombus:
A four-sided polygon with equal-length sides is called a rhombus. It has opposite angles equal and opposite sides parallel.

Trapezoid:
One pair of parallel sides make up the four sides of a trapezoid.

Pentagon:
The term “pentagon” refers to a polygon that has five sides and five angles. It has five corners and can be classified into different types based on the length of its sides and angles.

Hexagon:
A six-sided polygon with six angles is referred to as a hexagon. It has six corners and can be classified into different types based on the length of its sides and angles.

Heptagon:
Heptagons are polygons with seven sides and seven angles. It has seven corners and can be classified into different types based on the length of its sides and angles.

Octagon:
An octagon is a polygon featuring eight sides and eight angles. It has eight corners and can be classified into different types based on the length of its sides and angles.

Nonagon:
A polygon with nine sides and nine angles is known as a nonagon. It has nine corners and can be classified into different types based on the length of its sides and angles.

Decagon:
A polygon with ten sides and ten angles is known as a decagon. It has ten corners and can be classified into different types based on the length of its sides and angles.

Parallelogram:
The term “parallelogram” refers to a four-sided polygon with two sets of parallel sides. It has opposite sides equal in length and opposite angles equal.

Kite:
A kite is a four-sided polygon with two pairs of equal-length adjacent sides. One pair of opposite angles in it are equal.

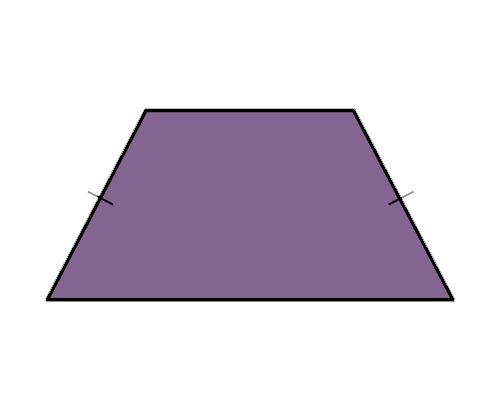
Isosceles Trapezoid:
An isosceles trapezoid is a four-sided polygon with two pairs of parallel sides. It has two adjacent sides equal in length.
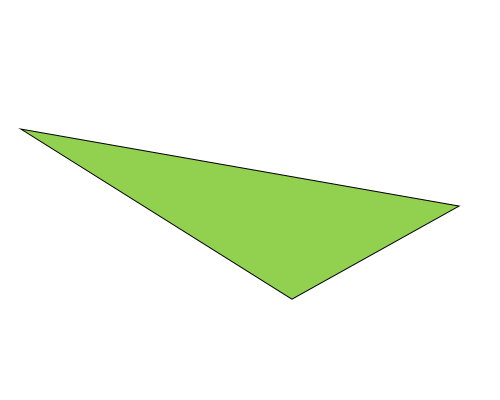
Scalene Triangle:
A triangle called a scalene triangle has sides of varying lengths.

Isosceles Triangle:
A triangle with two sides that are of equal length is said to be isosceles.

Equilateral Triangle:
A triangle with equal-length sides is said to be equilateral.

Right Triangle:
A right triangle is a three-sided polygon with one angle measuring 90 degrees.

Obtuse Triangle:
A triangle is said to be obtuse if one of its angles is more than 90 degrees.
Acute Triangle:
A triangle with all angles less than 90 degrees is known as an acute triangle.

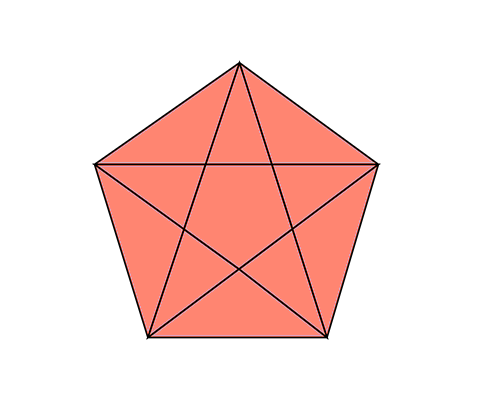
Pentagram:
A pentagram is a five-pointed star polygon, formed by five straight lines connecting the vertices of a regular pentagon.
Hexagram:
A hexagram is a six-pointed star polygon, formed by two overlapping equilateral triangles.

Octagram:
An octagram is an eight-pointed star polygon, formed by two overlapping squares.

Ellipse:
An ellipse is a curved shape that resembles a stretched-out circle. It is defined as the set of all points where the sum of the distances from two fixed points (foci) is constant.

Parabola:
A parabola is the graph of a quadratic function, and it is a U-shaped curve with a vertex that denotes where the curve changes direction.

Hyperbola:
A hyperbola is a curved shape that looks like two mirror images of each other. It is defined as the set of all points where the difference of the distances to two fixed points (called foci) is constant.

Cylinder:
A cylinder is a three-dimensional shape that has a circular base and a curved surface that goes up to a fixed height. It can be visualized as a can or a tube.

Sphere:
A sphere is a three-dimensional shape that has the appearance of a ball. The set of points equidistant from a fixed point, known as the center, defines it.

Cube:
A cube is a three-dimensional shape that has six equal square faces. It has eight corners and 12 edges.

Cuboid:
Having six rectangular faces, a cuboid is a three-dimensional shape. It has eight corners and 12 edges.

Pyramid:
A pyramid has a polygonal base and triangular faces that converge at a shared vertex, creating a three-dimensional shape. The base can be any polygon, and the most common are square and triangular pyramids.

Cone:
A cone is a three-dimensional shape that has a circular base and a curved surface that narrows down to a single point, also known as the apex. It can be imagined as an ice cream cone or a party hat.

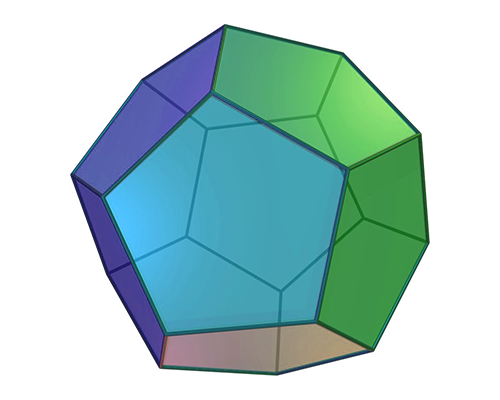
Dodecahedron:
With 12 regular pentagonal faces, 20 corners, and 30 edges, a dodecahedron is a three-dimensional shape.
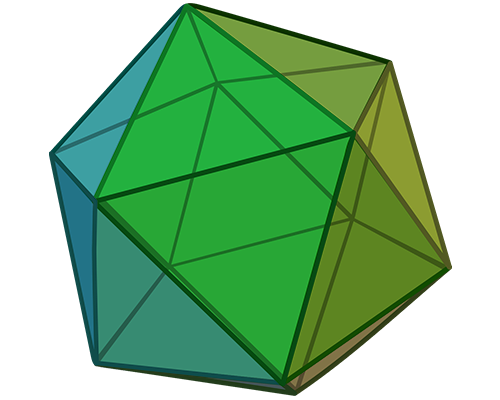
Icosahedron:
An icosahedron is a three-dimensional shape that has 20 equilateral triangle faces, 12 corners, and 30 edges.
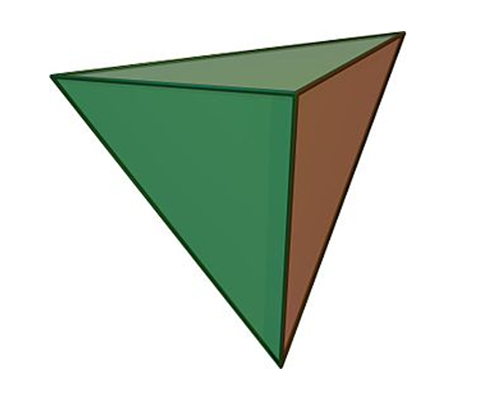
Tetrahedron:
A tetrahedron consists of four triangular faces, four vertices or corners, and six edges. It is a three-dimensional geometric shape.
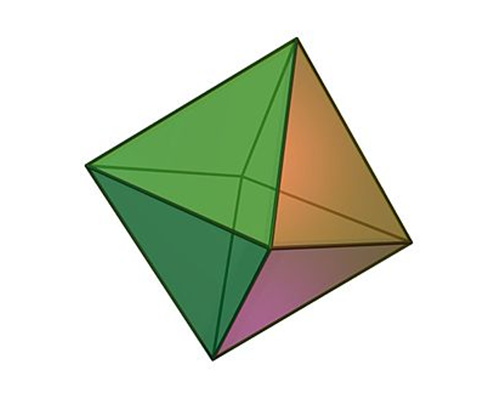
Octahedron:
An octahedron is a three-dimensional shape that has eight equilateral triangle faces, six corners, and 12 edges.
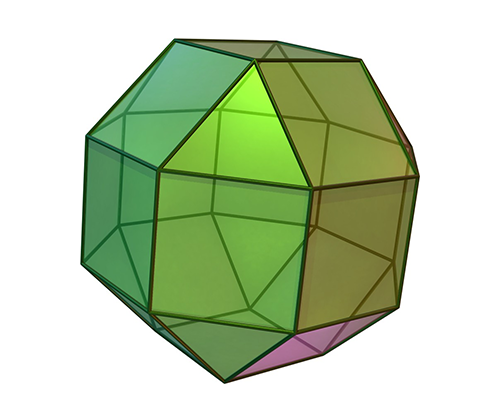
Rhombicuboctahedron:
A rhombicuboctahedron is a three-dimensional shape that has 26 faces, including 18 squares and eight regular triangles, 48 edges, and 24 corners. The shape is alternatively referred to as the “Inca stone” or “sacred geometry”.
Oval:
An oval is a curved shape with no straight lines or vertices, resembling the outline of an egg. It has one flat face.

Rectangular Prism:
A rectangular prism is a 3-D shape with six rectangular faces and twelve edges.

Arrow:
An arrow is a line with an arrowhead at one end, often used to indicate direction or provide guidance.

Crescent:
A crescent is a curved shape with two pointed ends, resembling the shape of a crescent moon.

Cross:
A cross is formed by the intersection of two lines at a 90-degree angle, creating a four-sided shape.

Heart:
A heart is a symbol with a shape resembling a stylized heart, often used to represent love or affection.

Quadrilateral:
A quadrilateral is a four-sided polygon with no sides or angles that are equal.

Ring:
A ring is a circular band often worn on the finger or used to hold something in place.

Semicircle:
A semicircle is half of a circle, with an angle of 180 degrees.

Star:
A star is a shape created by connecting multiple polygons to form a symmetrical, star-like pattern.

Trapezium:
A trapezium is a quadrilateral with two parallel sides and two non-parallel sides.

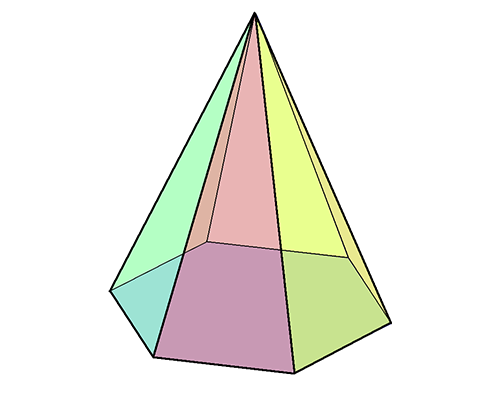
Hexagonal pyramid:
A hexagonal pyramid is a 3-D shape with a hexagonal base and six isosceles triangular faces joining at the top.
Prism:
A prism is a 3-D shape with parallel polygonal faces and rectangular lateral faces.

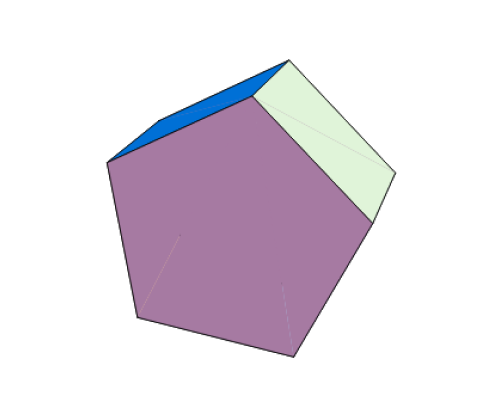
Pentagonal prism:
A pentagonal prism is a 3-D shape with two pentagonal faces and six rectangular faces joining them.
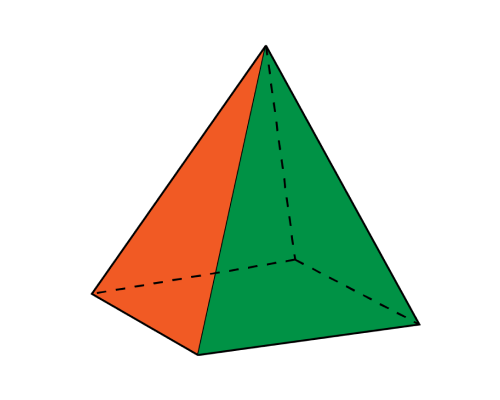
Square Pyramid:
A square pyramid is a pyramid with a square base and four triangular faces joining at the top.
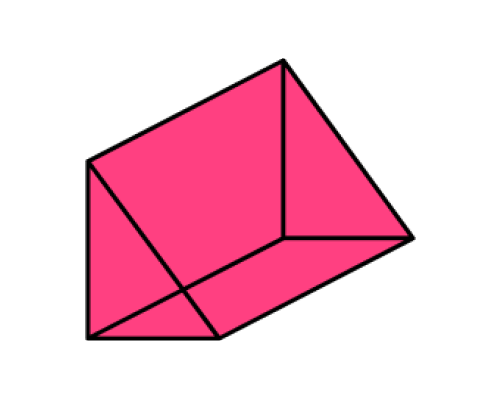
Triangular Prism:
A triangular prism is a 3-D shape with two parallel equilateral triangular faces and three rectangular lateral faces joining them.
Knowing the names of shapes and their properties is not only important for mathematical understanding but also useful in real-life situations. From construction to art, shapes play a vital role in our daily lives, and understanding their properties can help us appreciate their beauty and significance even more.
Read Also: Number Names for Kids


